n个元素进栈,共有多少种出栈顺序？

我们生活里可能有这种场景，哥哥在一旁洗碗，把洗好的碗直接摞在案板上，弟弟则把案板上洗好的碗在搬到橱柜里，问弟弟放碗会有多少种情况？这个问题跟上面问题是一致的。

当只有2个元素、3个元素时，我们可以用穷举法得出答案。但是一旦元素变多，穷举法这种方法就不可行了。

这个问题已经有推导出的公式了，如下所示：

h(n)=C(2n,n)-C(2n,n-1)

这里C是代表组合的意思，关于组合的概念及公式，不熟悉的话，可以观看我这篇文章：排列组合的概念及公式推导。

上面h(n)就是卡特兰数，也正是开篇那个问题的答案。

百度百科有归纳法的证明，这里不提这种方法，本文要讲解的是“折线法”。

为什么叫“折线法”，稍后你就知道了。

数学上有一种方法，就是将代数问题转为几何问题，简单点说，就是将生硬的文字说明变为图形来描述。

n个元素进栈,共有多少种出栈顺序？这个问题，可以先变为“一个有n个1和n个-1组成的字串，且前k个数的和均不小于0，那这种字符串的种数为多少？”这样更为直观的问题。“要求不小于0”是什么意思？意思就是栈里元素全部出栈后，如果没有元素接着进栈，那是不可能继续有元素出栈的。

理解了上面问题的转变，现在就将上面转变后的问题映射到数轴上，如下图所示：

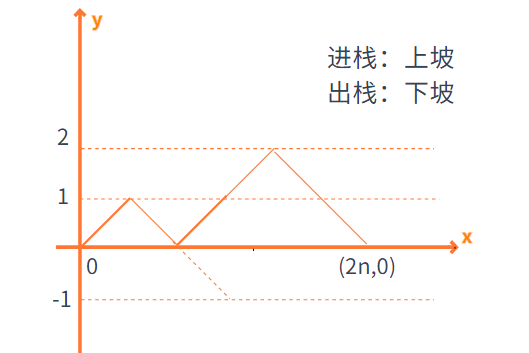
用右向上的线代表进栈，右向下的线代表出栈，那么n个元素，就有n次进栈n次出栈。

那么上面公式里C(2n,n)就好理解了，就是从2n个线条里挑出n个线条是向上的。

C(2n,n)里还包含折线与y=-1有交点的情况，这种情况不符合我们问题的要求，所以要排除掉，所以接下来的就是要算出C(2n,n)中有多少种情况是与y=-1相交的情况，然后把这些情况减掉。

从h(n)=c(2n,n)-c(2n,n-1)公式里我们已经知道与y=-1相交的情况有C(2n,n-1)种，那是怎么得出来的呢？请看下图：

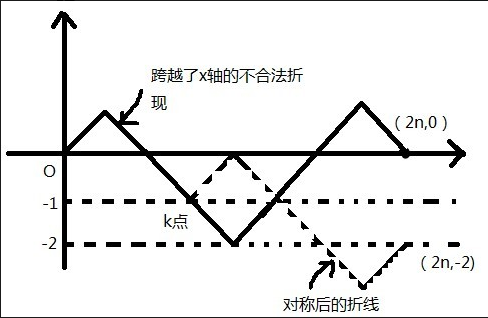
我们假定k点是第一个折线与y=-1相交的点，那么k点之后实际的折线，无论是怎样的，以y=-1作为对称轴，都可以将最终结点对称到(2n,-2)这个点（虚线是对称后的折线）。这个自行多画几种情况慢慢体会吧。

对称后的最终结点到了y=-2，说明了什么？说明了此种情况下，下坡线比上坡线多2条。正好总共2n条线，那么上坡线就是n-1条，下坡线n+1条。C(2n,n-1)这个组合就是这么来的，表示从2n条单元线中挑出n-1条作为上坡线的情况种数，即与y=-1会有相交的折线情况种数。

到此卡特兰数公式就证明完了。

回到最初，为何叫“折线法”？我想你看了图片就应该理解了。

但是翟码农现在想着感觉应该是排列，而不是组合，有兴趣的人可以帮我剖析剖析。

本文为翟码农个人博客蓝翟红尘下数学逻辑分类下有关卡特兰数公式理解证明的文章，转载请注明出处：

http://www.zhai14.com/blog/how-to-use-graphic-to-analyse-catalan-expression.html

• 2020年02月11日 17:09文章创建
• 2020年02月13日 22:45文章发布