抢红包算法之二倍均值法详细讲解

看了网上的很多人写了抢红包的这个二倍均值算法，可惜本人愚钝，总觉得看得不是很懂，所以只好自己钻研了。

本文只分析二倍均值法抢红包的算法思路，不写代码。本星期我将会将另开一篇，用来展示算法实现的代码。

首先让我们假定一下场景和要求。

场景：

我在微信里发总额200元的红包，包成10个小份的红包，发到微信群里让大家开始抢红包。

要求：

1. 参与抢红包的前10个人，必须每人至少能抢到1角。（考虑到后面算法思路里除以2会涉及小数，所以就考虑到角）

2. 红包必须被抢完，一分不多，一分也不少。

二倍均值法的思路：

1.200元红包，若平均包成10个红包，则红包的平均金额为200/10=20元。

2.然后前9次抢红包都是从0到40元这个范围里挑选随机值，然后再将随机金额值除以2。

3.最后一个红包就是红包剩下的金额。

在分析思路之前，先让我们证实下面结论：

一个线性区间范围的平均值，即是这个区间的中点值

线性只是我为了描述更加严谨而加上去的，为了分析简便，这里忽略它。

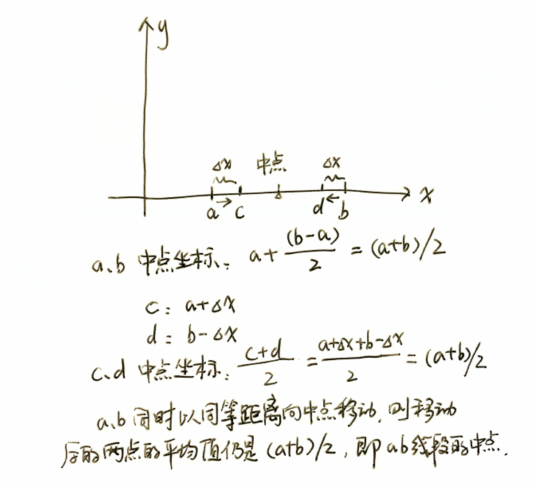
在数轴坐标系中，我们可以计算出x轴上a、b之间的中点坐标是(a+b)/2,这也正是a和b这两个值的平均值。

刚才只能表明a、b两点之间的点值是它们的平均值，适不适用于a、b之间的整个区间呢？

从a、b两端出发，以同等距离往中间靠近，由上可以得知，移动后两点的平均值仍然是a、b之间的中点值。一点点的移动，移动的点就形成了a、b整个区间，如此就可以看出，整个区间范围的平均值，也是这个区间的中点值了。

详细见下图：

二倍均值法为了保证抢红包游戏对于抢到红包的每个人是公平的，即每个人抢到同等红包金额的机会是相等的，采用了每个人抢红包金额的平均值要相等的这一标准。

场景里，每人抢到的平均值就得是20元才公平，正是思路里的第1步描述。

根据上面我们证实的结论，我们就可以确定每个人抢红包的金额区间范围了：(0, 40),这里括号表示不包括0和40这两个值。

那为何思路里第2步，只随机抢9次，而不是10次呢？

如果10次全部随机，就会导致不能满足场景的要求2：红包必须完完全全被抢完，不能留有剩余。所以就采用9次随机，剩余的作为就第10次的红包金额了。

随机范围确定好了，挑选出随机值后，干嘛又除以2呢？

如果为了公平，其实是不应该除以2的，但你想，如果前8个人每个人随机到25元，红包200元就已经被抢光了，这是不满足场景里的要求1的：每份红包必须得有钱，哪怕是1毛。

二倍均值法里每个人抢得同等红包金额的机会都是相等的吗？

如果思路里第2步，不除以2，我们还可以这样说。但除以2后，明显就变化了。

前9个人，红包金额区间(0,20), 平均值皆为10元。

最后一个人，红包金额区间(0,200),平均值为100元。

所以抢到红包的最后一个人抢到同等红包金额的机会是比前面其他人要大的，而且前面的任何人相互之间机会都是均等的。

实际抢红包，我们知道，微信群里人数总是大于红包个数的，所以要想成为抢得最后那一份红包的，也是得拼运气的：早一秒和晚一秒你都会与之擦肩而过的。所以，二倍均值法作为红包算法还是合理的，只是除了最后一个人，前面的每个人抢得的红包金额值都在指定的区间范围内，所以少了些刺激和惊喜。